Guillaume Martinet presents “Variance Minimization in the Wasserstein Space for Invariant Causal Prediction” with an oral at AISTATS 2022! We address the challenge of identifying causal features in prediction using the invariance assumption.
The Invariance Assumption states that the residuals of a regression problem remain invariant in distribution across samples when the causal variables are included in the model.
The challenge with the methods that perform causal inference under this assumption, most specifically (ICP](https://jstor.org/stable/44682904?seq=1), is that they test all subsets of features, leading to 2^p number of tests. This doesn’t work when there are p>10 features in a study.
Guillaume and Alexander reframed this problem as a multiple testing framework, and developed the Wasserstein variance to measure the variability of the residual’s distribution across samples. The testing framework only requires p tests, making it a linear problem.
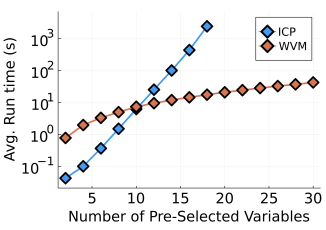
Furthermore, their elegant solution – Wasserstein variance minimization (WVM) – allows explicit testing of subsets of features, computing (for example) the likelihood that the causal features are contained within a larger set of features.
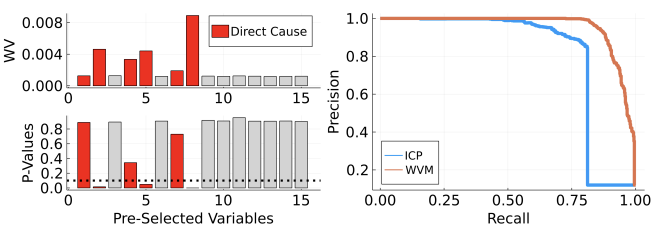
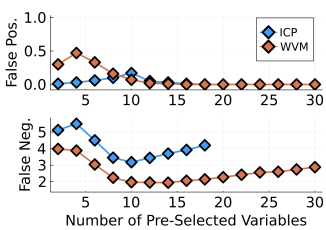
In simulations, WVM performed better than ICP even on small numbers of features, presumably because ICP’s output is the intersection of the results of 2^p tests, which can reduce its power in finite samples.